C程序设计实验报告实验项目：函数的定义和调用1、编写由三角形三边求面积的函数

2、编写求N阶乘的函数

3、求两个整数的最大公约数

4、打印输出指定图形

姓名：黄澄       实验地点： 514实验室       实验时间：2019年4月30日

一、实验目的与要求

1.编写由三角形三边求面积的函数调用area()函数求三角形的面积在求面积函数运用海伦公式

2、编写求N阶乘的函数定义符号常量使用长整型变量存放累乘积使用全局变量存放累乘积

3、求两个整数的最大公约数调用bcd()函数求两个整数的最大公约数掌握辗转相除法求两个整数的最大公约数

4、打印输出指定图形调用trangle()函数输出三角形trangle()函数中用for循环的嵌套输出指定的结果

5.模块化程序设计编制一个函数facsum(m),返回给定正整数m的所有因子(包括1但不包括自身)之和编制一个主函数，调用(1)中的函数facsum(),寻找并输出500以内的所有亲密数对输出要有文字说明。在输出每对亲密数时，要求从小到大排列并去掉重复的亲密数对所有函数中的循环均为for循环

二、实验内容

1.问题的描述：

编写程序，从键盘输入三角形的3条边，调用三角形面积函数求出其面积，并输出结果。

2.流程图：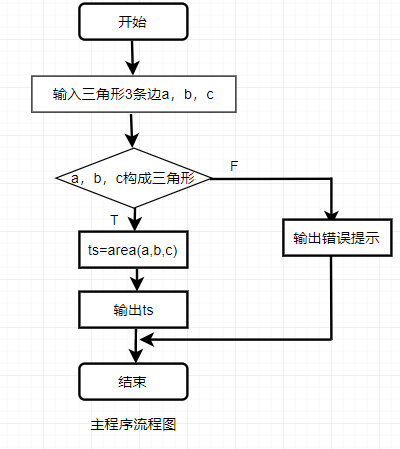

#include
    
     #include
     
      float area(float a,float b,float c){    float s,p,area;    s=(a+b+c)/2;    p=s*(s-a)*(s-b)*(s-c);    area=sqrt(p);    return(area);}main(){    float x,y,z,ts;    scanf("%f,%f,%f",&x,&y,&z);    ts=area(x,y,z);    if((x+y>z)&&(x+z>y)&&(y+z>x))    printf("area=%f\n",ts);    else printf ("date error!");}
     
    

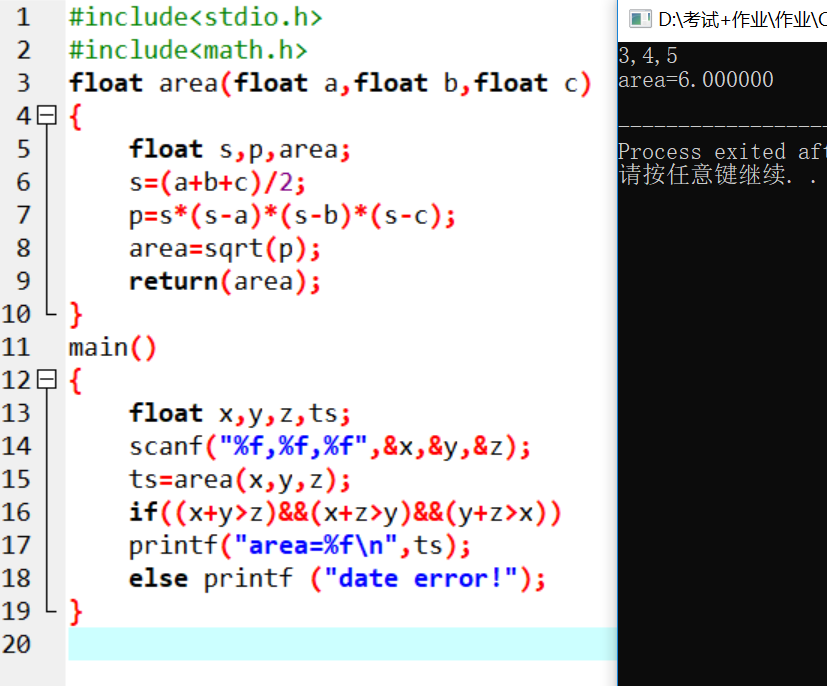
4.问题分析

运用了海伦公式以及两边之和大于第三边，海伦用了开方，头文件要包含<math.h>,两边之和大于第三边之间的关系用和。

6.4.1.2、编写求N阶乘的函数

1.问题的描述：

编写函数，求出从主函数传来的数值i阶乘值，然后将其传回主调函数并输出

2.流程图：

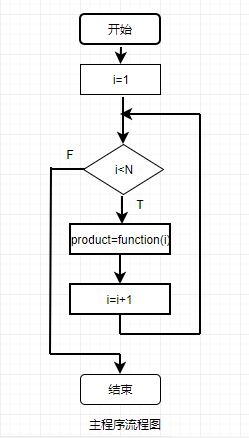
3.实验代码：

#include "stdio.h"#define N 5long function(int i){    static long f=1;    f=f*i;    return f;}int  main(){    int  product;    int i;    for(i=1;i<=N;i++)    {        product=function(i);        printf("%d的阶乘是：%d\n",i,product);            }}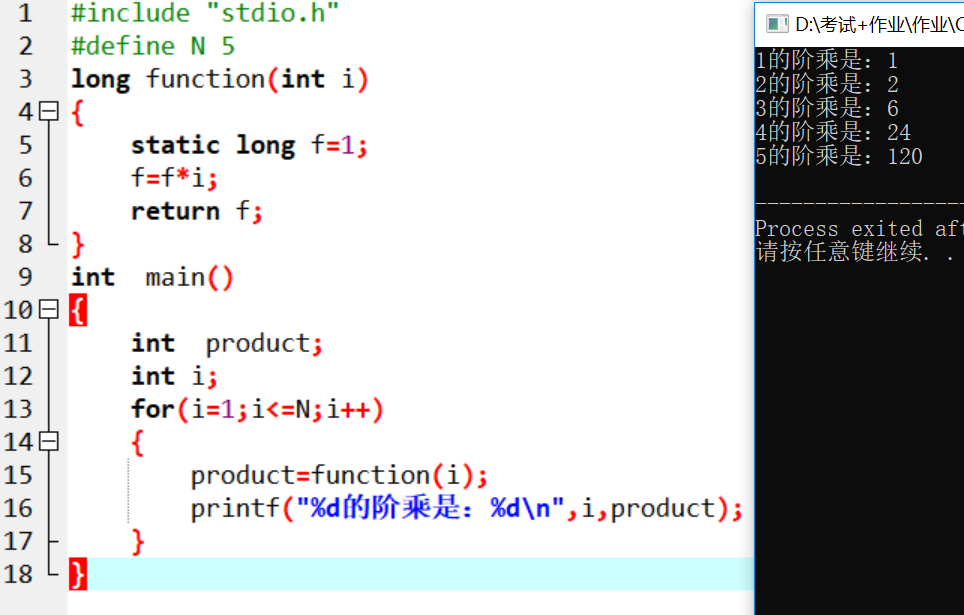

4.问题分析

局部静态变量的值具有继承性，利用这一特点就可以求出1~N的阶乘。每一次循环调用一次函数，该值是不会被释放的。

6.4.1.3、求两个整数的最大公约数

1.问题的描述：

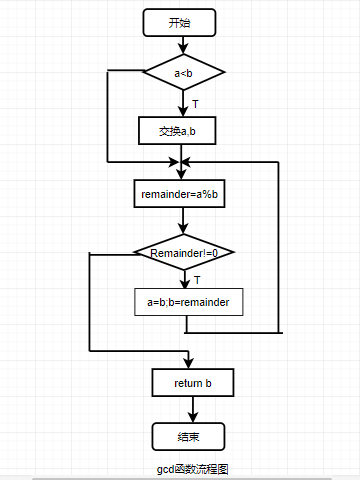
编写程序，从键盘输入两个整数，调用gcd()函数求他们的最大公约数，并输出结果。

2.流程图：

实验代码

#include 
    
     int gcd(int a,int b){    int temp;    int remainder;    if (a
    

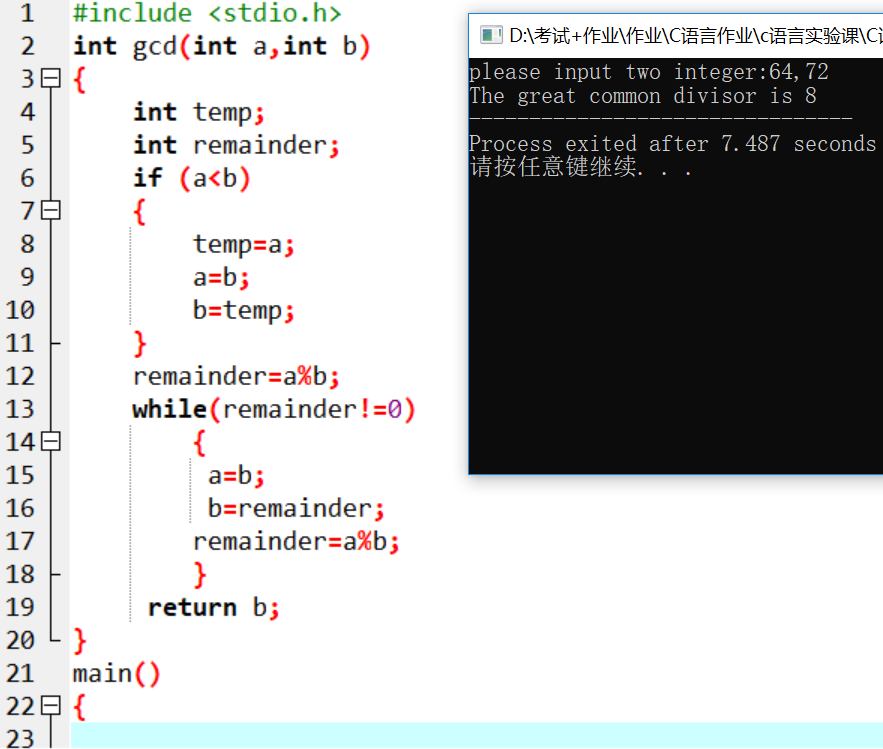
4.问题分析：

程序的关键点是辗转相除法求两个数的最大公约数，例如a>b，a除以b等于零，最大公约数就是b，不等于零的话就要用b继续除以这个余数如此反复直到为零，最后一个非零数就是最大公约数。因此while之后需要加入remainder=a%b;

6.4.1.4、打印输出指定图形

1.问题的描述：

输入整数n，输出高度为n的等边三角形，当n的值为5，等边三角形为： 

   

 

 

**** 

**********

2.流程图：

3.实验代码：

#include
    
         void trangle(int n)    {        int i,j,k;        for (i=0;i<=n;i++)        {            for (j=1;j<=(n-i);)            {                printf("#");                j++;            }            for(k=1;k<=(2*i-1);k++)            printf("*");            putchar('\n');        }        }        main()    {        int n;        printf("请输入一个整数：");        scanf("%d",&n);        printf("\n");        trangle(n) ;    }
    

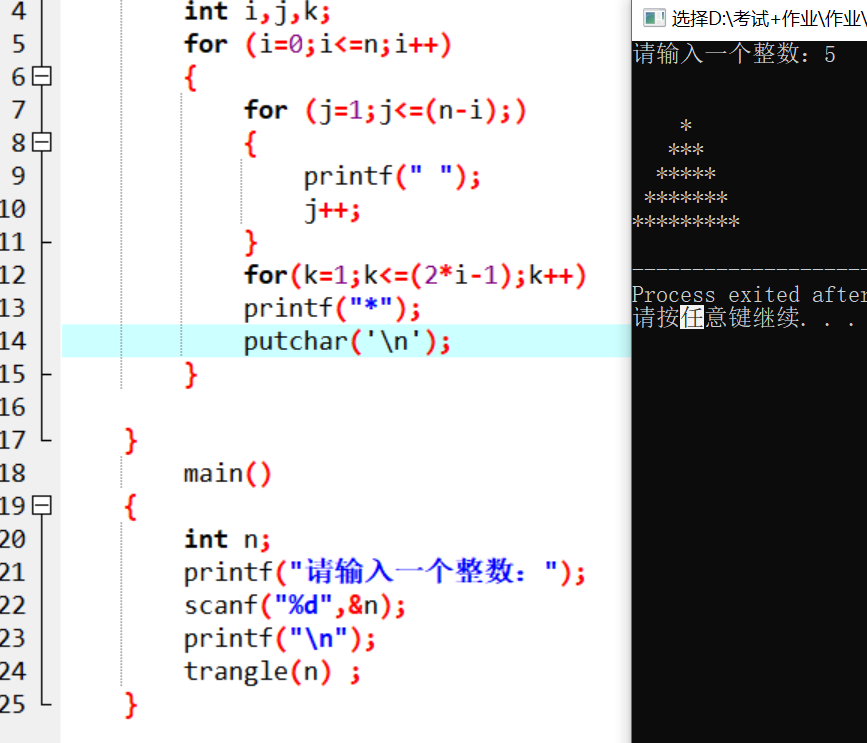
4.问题分析：

每一行星号前的空格都比上一行的少一个，每一行的星号个数也是有规律的，可以用2i-1来表示n表示行，i表示第几行，而j表示，我们可以发现图形总共有5行，第一行前面是4个空格，第二行3个空格，第三行2个空格······以此类推可以知道j=n-i，然后j<=2i，根据这个规律编写一个trangle（）函数，然后在调用该函数就可以打印出高度为5的等边三角形。

6.4..2.1模块化程序设计

1,问题描述

若正整数A的所有因子（包括1但不包括自身，下同）之和为B，而B的因子之和为A，则称A和B为一对亲密数。例如，6的因子之和为1+2+3=6，因此6与6为一对亲密数（即6自身构成一对亲密数）；又如，220的因子之和为1+2+4+5+10+11+20+22+44+55+110=284，而284的因子之和为1+2+4+71+142=220，因此，220与284为一对亲密数。求500以内的所有的亲密数对。

2、流程图

3.实验代码

#include 
    
     int facsum(int m){    int sum=1,f=2;    while(f<=m/2)    {        if(m%f==0)              sum=sum+f;              f=f+1;    }    return sum;}main(){    int m=3,n,k;    while(m<=500)    {        n=facsum(m);        k=facsum(n);        if (m==k&&m<=n)        printf("%d %d\n",m,n);        m++;    }}
    

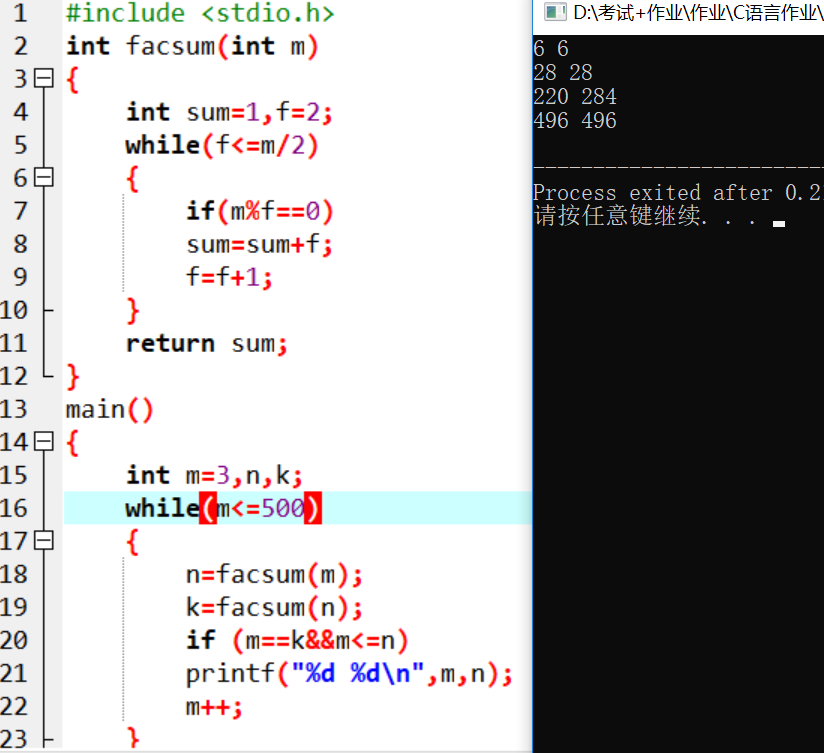
4.问题分析：

在facsum(m)模板中，求出m的所有因子，并将它们的和作为返回值，在主函数中，for循环从m=3开始调用函数，再计算m是否有亲密数对

三、实验小结

这里学到了几点。1.海伦公式以及求面积的函数类型是浮点型，他是有返回值的，不能写成调用语句，把函数调用当做表达式。能把他放在表达式能出现的任何地方。2、辗转相除法的用法。3、局部静态变量的值具有继承性，利用这一点特性就可以求连续的值了。4、模块化程序设计思维